京都医塾数学科の福本です。
前回に引き続き、今回もユークリッドの互除法の解説を進めていきます。
前回のおさらい
自然数a, bの公約数を求めたいとき、
① 縦・横の長さがa, bであるような長方形を考える
② ①の長方形をぴったり埋め尽くす、1辺の長さがcの正方形を見つける(cは自然数)
③ cはaとbの公約数である
④ cの中で最大のものが最大公約数である(これを探す方法がユークリッドの互除法)
「2数の最大公約数を求める」ことは「長方形を埋め尽くす最大の正方形を見つける」ことに置き換えることができます。
<ユークリッドの互除法の図形的手法>
整数a, bの最大公約数を求めたいとき、
① 縦・横の辺の長さが、それぞれa , bの長方形をかく。
② 短い方の辺で正方形を作り、長方形の中にできるだけ沢山埋める
③ 正方形が埋まりきらずに余った場合、残り部分の長方形の中で ②の操作を繰り返す
この手順で、長方形を埋め尽くす最大の正方形を見つけることができます。
それでは、前回の記事で例として挙げた問題
(例題)360と165の最大公約数を求めよ
について、実際に図形を用いて考えてみましょう。
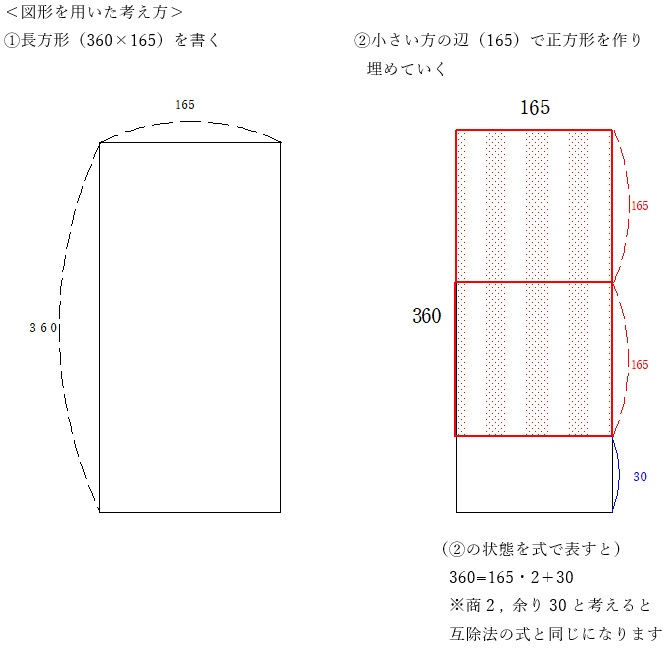
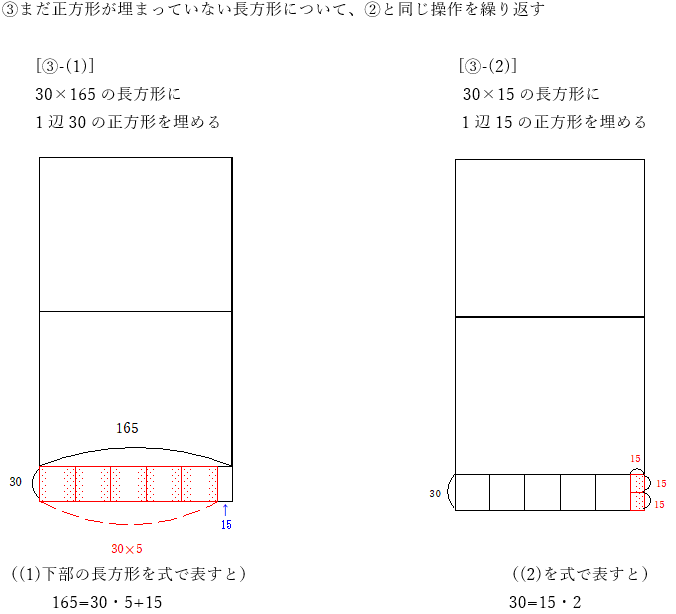
以上のような操作から、360×165の長方形は「15×15の正方形で埋め尽くせる」ことがわかります。さらに、この正方形は、360×165の長方形を埋め尽くせる正方形のなかでは最大のものとなります。
これで360と165の最大公約数は15であることがわかりました。
前回の記事では、この問題を例として互除法の使い方を紹介しました。
(例題)360と165の最大公約数を求めよ
360=165・2+30
165=30・5+15
30=15・2
数式のみの解答と見比べても、それぞれの図形に対応した式が出ていることがわかります。
まとめ
以上が、ユークリッドの互除法のイメージとなります。
図形を用いた方法では、手順②で行う分割作業が多くなればなるほど図が書きづらくなっていきます。入試においては、ここから更に解き方を発展させ、数式による処理で問題を解く力を身につけていく必要があります。
大切なのは、分からないこと、難しいことをそのまま鵜呑みにするのではなく、まずは入門としてイメージから入ってみること、別方向の見方からアプローチしてみることです。学び方は一つではない、ということが、数学の面白さの一つでもあります。
京都医塾では、たとえ同じ内容の事柄であっても、生徒の理解度に合わせて異なる教え方をすることがあります。「自分が良いと思う方法」だけにこだわらず、臨機応変に説明を変えることができる。それが医塾の講師の良いところです。
このブログを見ている生徒の皆さんも、分からないところ、悩んでいるところがあれば、ぜひ積極的に質問に来てくださいね。
京都医塾ではご相談・体験授業を随時募集しています。下記リンクからお気軽にお問い合わせください。



