京都医塾数学科の福本です。

今回は、場合分けの使い方について、実際の入試問題に触れながら解説していきたいと思います。

場合分けをして、解答への道筋を開く

問題を解く際には、場合分けを行うことで解答の道筋が見えやすくなることが多々あります。場合の数・確率や2次関数の最大最小の問題など、場合分けを使って解く問題は多く存在しますが、模範解答に示されているからそう解いているだけで、その重要性を意識したことはない、という受験生は意外と多いのではないでしょうか。

解答には表れない思考の部分で、このような「場合分けの力」が成否を分けることがあります。

基本知識の確認

問題に入る前に、１つだけ重要な知識を確認しておきます。

「すべての実数a, bに対して、a＞bまたはa<bまたはa=bの、いずれか１つだけが成り立つ」…☆

当たり前、と思う人もいるでしょうが、この当たり前を明確に認識することが数学の学習の第一歩となります。

杏林大学医学部の問題で実際に解いてみる

実際に、本年度（2022年度）杏林大学医学部の問題Ⅲ(1)の一部を用いて、場合分けの使いどころを確認してみましょう。

Ⅲ

(1)座標平面上の3点A(－1,0)，B(1,0)，Cを頂点とする三角形について考える。

点Cの座標は正であり、原点をOとして、以下の問いに答えよ。

(a) ∠BAC＜∠ABC を満たす場合、点Cは第[  ア  ]象限にある

＜2022年度　杏林大学医学部　問題Ⅲ(1)より抜粋＞

問題はこの後も続きますが、まずはここだけを考えてみましょう。

パッと見て、どんな状況かいまいちわからないな、と感じた人もいると思います。

この問題を解きにくくしている要因は、なんといっても不等式（＜）で角の値の関係が表されていることに尽きます。

ここで、先ほどの☆の理論を思い出してみましょう。たとえ角度どうしの関係であっても、それらの値が実数である以上、☆は成り立ちます。

☆をこの問題中の言葉を用いて言い換えると、

「∠BACと∠ABCは、∠BAC＜∠ABCか、∠BAC＞∠ABCか、∠BAC＝∠ABCのいずれか１つの関係で表せる」

となります。

これは、点Cの位置によって変化する角度の値は、上記3パターンのいずれかに必ずあてはまる（だからそれで場合分けすればよい）ということを表しています。

ここで皆さんに質問です。

(ⅰ)∠BAC＜∠ABC

(ⅱ)∠BAC＞∠ABC

(ⅲ)∠BAC＝∠ABC

この中で、最も考えやすいのは、どの場合でしょうか。

おそらく、大半の人は(ⅲ)と答えるはずです。

結局、実数の大小関係がこの3つしかない以上、この中で最も考えやすい「＝」のパターンから調べていけば良いわけです。

問題の中で∠BAC＝∠ABCとなるときを考えてみると、

底角が等しいので、△ABCはAB=ACの二等辺三角形になることがわかります。

問題文より、点Cのy座標は正なので、必ずx軸よりも上に存在するということも加味して図示すると、以下のようになるでしょう。

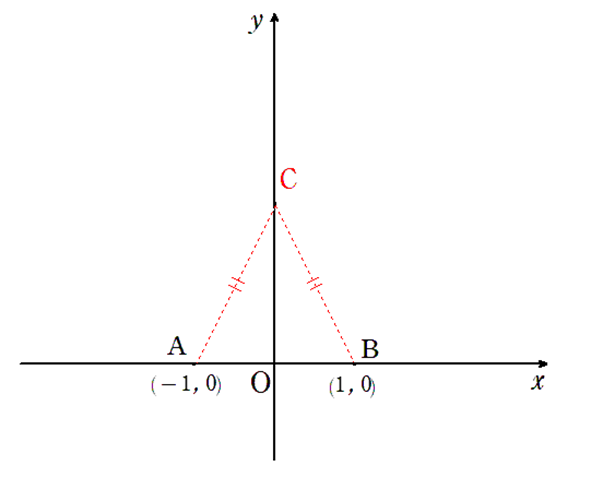
点Ｃがy軸上に存在するとき「∠CAB＝∠CBA」であることが分かりました。

こうならないとき、すなわち「点Ｃがy軸上から少しでもズレた位置に存在する」とき

「∠CAB＜∠CBAか∠CAB＞∠CBA」となります。

では実際に、点Ｃをy軸よりも右（第一象限）にずらしてみましょう。

すると、明らかに∠Bが、元の状態よりも大きくなり、∠Aは元よりも小さくなることが分かります。

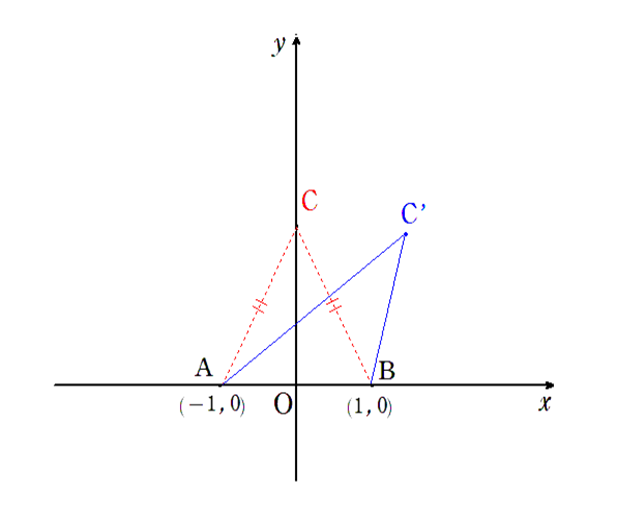
∠CAB=∠CBAの状態から、

・∠CAB→∠C’AB（小さくなる）

・∠CBA→∠C’BA（大きくなる）

と変化するわけですから、当然∠C’AB＜∠C’BAとなります。

これが、問題(a)で想定されている状況であるため、「第1象限」が答えになります。

※点Cをy軸から左（第2象限）に移した場合は、同様に、

∠CABが大きくなり、∠CBAが小さくなるので、∠CAB＞∠CBAとなります。

次に、この問題を見てみましょう。

「 (b)∠ABC＜∠ACBを満たす場合、点Cは[  イ　]の[　ウ　]に存在する 」

煩雑になるため具体的な選択肢は省略しますが、

イの中には円・楕円・正三角形・正方形のいずれかの図形、

ウの中にはその図形の内部・周上・外部・重心の、いずれかが入ります。

ここで、(a)で考えた状況を思い出してみましょう。

やはり、大or小の状況よりも「＝」の方が考えやすそうです。

「∠ABC＝∠ACB」となるのは、(a)同様、二等辺三角形となるときです。

ABの長さは一定（2）なので、ACの長さも常に同じ値（2）を取らなくてはなりません。

つまり、点CはAを中心とした円周上を動くことになります。

ここまでわかれば、解答の道筋が見えてきそうです。

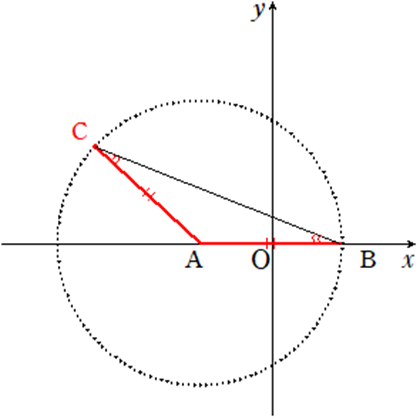
この段階で、「＝のとき周上」「＞or＜のとき外部or内部」という対応関係に気付ければ、より解きやすいでしょう。

求めたいのは∠ABC＜∠ACBのときなので、「∠ABC＝∠ACB」つまり「点Cが円周上にある」状態からズラしてみることにします。

「点Cが円の外部にあるとき」

(a)よりも少し難しいですが、点Cが第一象限の「右下の方」にあるときなどの、極端な形を考えてみると分かりやすくなります。

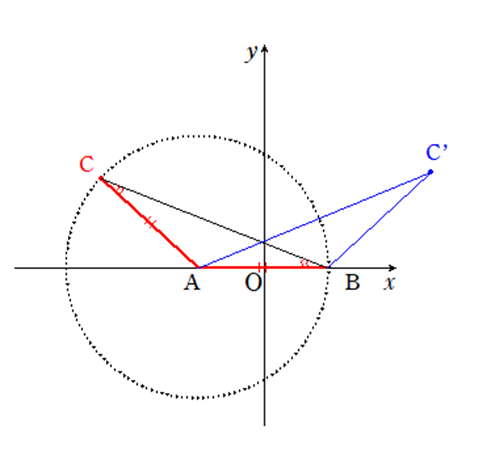
このような円の外部の点C’を取ってみると、明らかに∠AC’B＜∠ABC’となります。

これで、

・∠ACB＝∠ABCのとき、周上

・∠ACB＜∠ABCのとき、外部

であることが分かりましたので、

・∠ABC＜∠ACBのときは、内部

も自動的に分かります（これが(b)の答えです）。

この後に続く(c)も、やはり同じ考え方で解くことができます。

また、(d)に関しては(a)~(c)で求めた領域中、共通する部分（「かつ」の条件）を取り出すことで解答を導くことができます。

ぜひ一度、自分で問題を確認したうえで、続きも解いてみてください。

今年の杏林大学の大問Ⅲは他の大問と比べて難易度が高く設定されていましたが、(1)のみに関していえば、上述のような論理が身についていれば、図形の知識がそこまでない受験生でも解ける問題と言えるかもしれません。

まとめ

有名なデカルトの格言に「困難は分割せよ」という言葉があります。

場合分けは、まさにこの「分割」を行うための有効な方法の1つであるといえるでしょう。

難しい問題にあたったときは、ぜひ皆さんも「分割して」解いてみてください。