「こんな問題があれば勉強になるはず！しかし、理想の問題が手元にない！」

数学講師の悩みといえば、目の前の生徒たちにとって最も学習効果のある問題を演習させたいにもかわからず、問題集やデータベースを漁っても最適な問題が見つからないことです。

そこで「ないなら作ってしまえば良い！」と作問(問題作成)に向かう講師も多いです。

今回は”裏側”紹介のようになってしまいますが、実は受験生であっても作問が効果を発揮することがあるので、そのことを実感していただくためにも実際に筆者が最近行った作問の風景をご紹介します。

「こんな問題を作りたい」を頭の中に書き出す

たとえば「媒介変数表示された曲線で囲まれた面積の問題を作りたい」と言っても様々なこだわりが出てきます。以下は実際筆者が考えたことです。

①　”折り返し”がある曲線にしたい。つまり \(x\) も \(y\) も単調に変化するだけではないようにしたい。

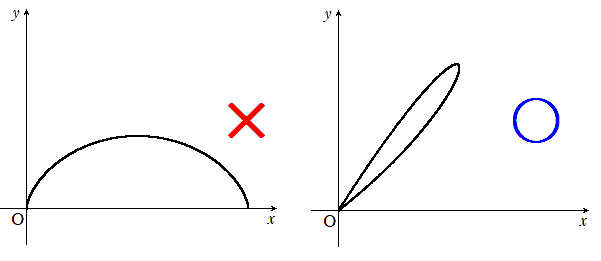
②　最後に媒介変数を用いて置換積分したときに「計算量は多くないが盲点になりやすい積分計算」をさせたい。

③　増減表作成に時間がかからないように \( \displaystyle \frac{dx}{dt} \) , \( \displaystyle\frac{dy}{dt} \) を簡単に計算できるようにしたい。

④　簡単に媒介変数を消去できる問題は避けたい。

⑤　「”実は”媒介変数を消去する解法もある」と生徒に言いたい。

よくばりですね。最後の1つに関しては蛇足に見えますが、こういう遊び心も忍ばせておきたいのが講師の心情です。

実際に作った問題

媒介変数 \(t\) を用いて表される曲線 \(C\): \(\displaystyle x=2\sin \left( t+\frac{\pi}{2} \right) \) , \(\displaystyle y=2\sin \left( t-\frac{\pi}{6} \right) \) ( \( 0≦t≦2\pi \) )

で囲まれた部分の面積 \(S\) を求めよ。

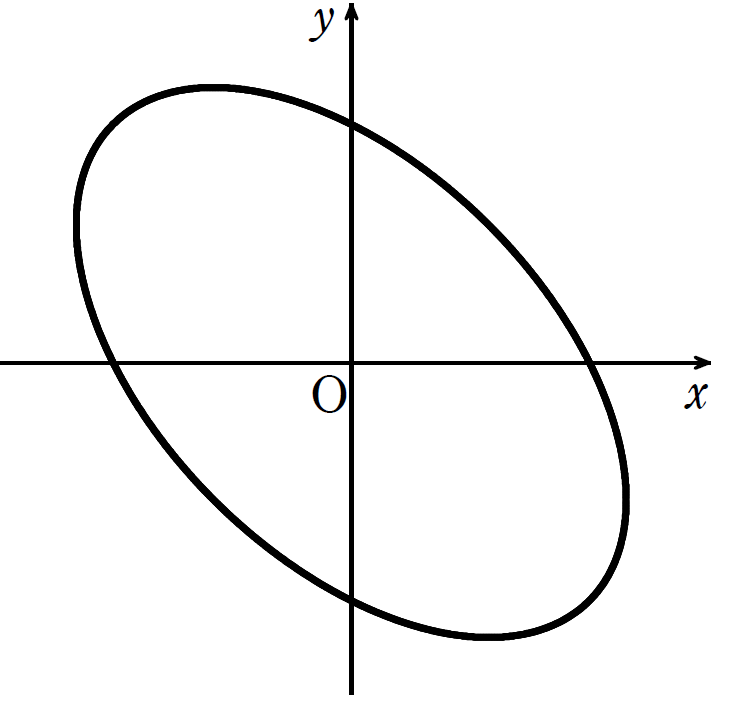
試行錯誤

「①折り返し」「②媒介変数が複雑すぎない」という条件を考えたとき、楕円の媒介変数表示が思い浮かべられます。

\(x=a\cos t\), \(y=b\sin t\)

しかし、これでは「④簡単に媒介変数を消去できない」に反します。

ということで失敗になるわけですが、ここで次のように考えます。

「たとえば \(5x^2+2xy+y^2=4\) で表されるような楕円であれば、容易に媒介変数を消去できない。ならば \(x=a\cos t\), \(y=b\sin t\) で表される楕円を回転させてしまおう。」

さて、この発想を実現させるためには「図形を回転させる方法」が必要になります。

今回は複素数平面の知識を用いました。

少し微調整なども加えた結果ですが

\(x= \sin t +\sqrt{3}\cos t \) , \(y=\sin t -\sqrt{3}\cos t \)

となりました。

これで大枠は完成です。しかし「④簡単に媒介変数を消去できない」という点が完全に解消されたわけではありません。

というのは先述の関係式の各辺を足したり引いたりすれば

\( 2\sin t = x+y \) , \( 2\sqrt{3}\cos t = x-y\)

という等式が得られますが、これらと \(\sin^{2}t+\cos^{2}t=1\) を用いれば \(x , y\) の関係式が容易に作れるからです。

そこで式変形を隠すために三角関数の合成を用います。

すると

\(\displaystyle x=2\sin \left( t+\frac{\pi}{3} \right) \) , \(\displaystyle y=2\sin \left( t-\frac{\pi}{3} \right) \)

と書き換わります。

これで媒介変数を消去する発想は生まれにくくなりました。

さらに「⑤”実は”媒介変数を消去できる」という条件も満たしています。

さて完成形とほぼ同じ形の式になりましたが、まだ完成ではありません。

「①折り返し」は確かに作れていますが、このままだと \( 0≦t≦2\pi \) の範囲で \( \displaystyle \frac{dx}{dt} \) の符号が変化する箇所が2か所になってしまいます。( \( \displaystyle \frac{dy}{dt} \) についても同様です。)

それでは「③増減表作成に時間がかからない」に反してしまいますし、面積の立式の際に面倒になってしまうことは明白です。

そこで媒介変数をずらすという処理を行います。

\(x , y\) の両方が最小の正の周期 \(2\pi\) である \(t\) の三角関数です。

そのためどちらも \(t\) を \(t+a\) ( \(a\) は実数) に置き換えても概形に変化は出ません。

そこで現時点で \( \displaystyle \frac{dx}{dt}=0 \) となる \(t\) の値のひとつである \( \displaystyle \frac{\pi}{6} \) を利用して

\(t\) を \(\displaystyle t+\frac{\pi}{6}\) に置き換えます。

\(\displaystyle x=2\sin \left( t+\frac{\pi}{2} \right) \) , \(\displaystyle y=2\sin \left( t-\frac{\pi}{6} \right) \)

ついに完成しました。

なお「②積分計算は計算量が多くないが盲点になる解法」という点に関しては三角関数の和積公式が使えるということを途中で確認しているために密かに条件を満たしています。

まとめ

やや難易度の高い問題でしたが、「媒介変数で表された曲線の面積」の問題を1つ作成するだけでも「複素数平面」や「三角関数」など、様々な知識をフル稼働させる必要があります。

高度な勉強法ですが、作問が受験生にとっていかに学習効果があるかがわかるかと思います。

もちろん、まずは「問題を解けるようになること」が最も重要ですが、「問題集の問題が解き終わってつまらない」という方はぜひ作問にも取り組んでみて下さい。

(おまけ)

今回の問題の答えは \(2\sqrt{3}\pi\) です。