突然ですが問題です。

共通テストで出題されそうな「データの分析」の問題ですが、次のように考えた人はいませんか。
相関係数 \(r\) は \(x,y\) の共分散 \(s_{xy}\) および \(x\) の標準偏差 \(s_{x}\) や \(y\) の標準偏差 \(s_{y}\) を用いて \(\displaystyle r=\frac{s_{xy}}{s_{x}s_{y}}\) と表されるから、共分散や標準偏差を頑張って表から計算すれば求められるはず…。
実はこの考え方には致命的な問題点があります。
それは「あまりにも時間がかかりすぎてしまうこと」です。
単に趣味の範囲で相関係数を計算するならまだしも、共通テストをはじめとした入試においては「早く正確に」問題を解くことが必要です。
そこで今回は以下のように解きます。
(1) 20個のデータをもとに自分で散布図を描く
(2) 散布図から「強い正の相関」or「強い負の相関」or「相関はほとんどない」を読み取る
(3) 選択肢から正しい答えを選択する
この解法を聞いて「そんな方法では相関係数を厳密に計算できないじゃないか」という”ツッコミ”が入るかもしれません。
おっしゃる通りです。
しかし、実は何の問題もありません。
なぜなら今回の問題は「正しい相関係数を選ぶ問題」だからです。
さて、実際に散布図を描いてみましょう。
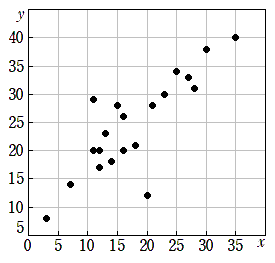
もっとおおざっぱに描いても問題ありません。
上の図のようになります。
すると「強い正の相関」であると自信を持って答えられるはずです。
したがって【問題】の正しい答えは③になります。
いかがでしょうか。
実際に描いてみると分かりますが、今回紹介した解法でこの問題を解くのに時間はあまりかかりません。さらに、多少打つ点がズレても正しい答えが選べます。
今回のように「データの分析」の問題を素早く処理するときには全体像をざっくりと読み取るという技があります。
もちろん分散の定義や相関係数の定義を覚えてきちんと計算することもデータを精密に解析する上では重要ですが、情報を視覚化してデータの散らばり具合、関係性、傾向をつかむことも「データの分析」では重要です。
その意味でデータの分析では、ある意味”ノリ”も大事だと言えるかもしれません。
皆さんも「データの分析」の問題を解くときに全体像をざっくりと読み取ることも解法の選択肢に入れてみて下さい。


