ユークリッドの互除法の図形的な捉え方(前編)

京都医塾数学科の福本です。

今回は、数学A「整数の性質」の重要定理である「ユークリッドの互除法」について、図を用いて解説していきたいと思います。

＜互除法の原理とは＞

2つの自然数a, b について（ただし、a>bとする）

aをbで割った余りをr（r≠0）とすると、

aとbの最大公約数とbとrの最大公約数は等しい

この原理は、2つの自然数の最大公約数を見つけるために使います。

実際に互除法を利用して公約数を求めると、以下のようになります。

（例題）360と165の最大公約数を求めよ

360=165・2+30（このとき、360と165の最大公約数は165と30の最大公約数に等しい）

165=30・5+15

30=15・2

よって、360と165の最大公約数は15

このような流れで最大公約数を求めることができます。

上記の計算は、不定方程式の特殊解を求めるときなどにも役立ってくれます。

何をやっているのかよくわからない、あるいは、問題は解けるものの、なぜこれで最大公約数が求められるのか理解できない、という人は多いのではないでしょうか。

この、一見すると複雑な互除法の考え方ですが、図形を用いて考えてみると、案外簡単に理解することができます。

互除法の説明に入る前に、まずは「2つの自然数の公約数」が「長方形と正方形」という図形を用いて、どのように表されるのかを考えてみましょう。

（例）30と15の公約数について考える

◎30と15の公約数の１つに、5がある。

1辺の長さが5の正方形は、縦, 横の長さがそれぞれ30, 15である長方形をぴったりと埋め尽くすことができる。

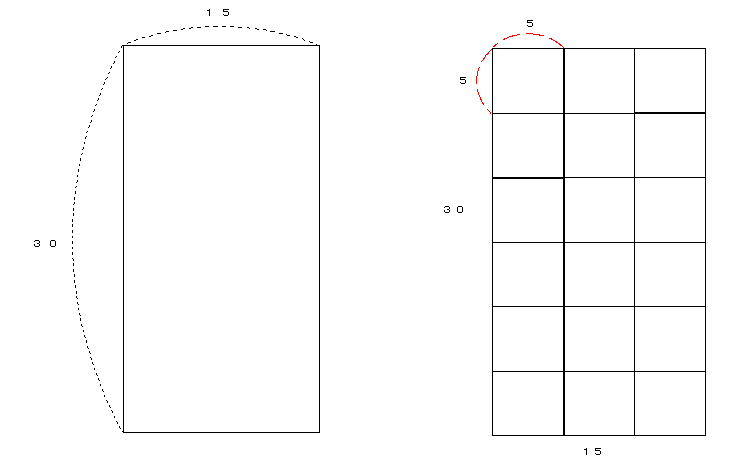
もちろん、1辺5以外にも、3や15あるいは1といった長さを持つ正方形は、上記の長方形をきれいに埋め尽くすことができます。

もしも、このような正方形のうちで最大のもの（ただし、1辺の長さは自然数）が見つかれば、それが最大公約数となるわけです。

このようなイメージをもって見ると、ユークリッドの互除法は「長方形を埋め尽くすことができる正方形の中で最大のもの」を見つける方法であると言えます。

自然数a, bの公約数を求めたいとき、

① 縦・横の長さがa, bであるような長方形を考える

② ①の長方形をぴったり埋め尽くす、1辺の長さがcの正方形を見つける（cは自然数）

③ cはaとbの公約数である

④ cの中で最大のものが最大公約数である（これを求めるのがユークリッドの互除法）

次回は、ユークリッドの互除法を「長方形と正方形」で解説していきます。