こんにちは、京都医塾化学科の児玉です。

前編では、質量保存の法則、定比例の法則、原子説、倍数比例の法則の4つの法則を説明していきました。

それでは、今回は気体反応の法則と、現代でも広く知られている分子説について説明していきます。

５．気体反応の法則

1808年に、フランスの科学者ゲーリュサックが発見した法則です。
ゲーリュサックは、様々な気体同士の反応を調べた結果、
「気体どうしの反応では、同温・同圧のもとで、反応に関係する気体の体積の間には簡単な整数比が成り立つ」という法則を発見しました。これを気体反応の法則と言います。
例えば、水素と酸素が反応して水蒸気が発生する反応で考えると、反応した水素と酸素の体積と、生成した水蒸気の体積との間の体積比は、同温・同圧では2：1：2となります。

この法則も法則名と法則の中身がリンクしているので覚えやすいですね。皆さんも暗記できていると思います。

原子説の矛盾

ゲーリュサックは、自分で発見した気体反応の法則の法則を、当時発表されていた原子説に基づいて説明をしようとしましたが、なかなか上手く説明することが出来ませんでした。
当時、「水素と酸素はそれぞれ水素原子、酸素原子からできている」ということと、「水蒸気は水素と酸素が一定の割合で結びついた複合原子である」ということは分かっていたため、これらに基づいて、水素と酸素、水蒸気の反応では、それぞれの体積比は2：1：2となる原理を説明をしようとしましたが、

(ⅰ) 下図のように、「体積比が2：1：2である」ことに重きをおいて考えると、

このように、酸素を半分に分割することになってしまい、原子説の(1)すべての物質は、それ以上分割できない微粒子からなるということに矛盾してしまいます。

(ⅱ) 今度は、下図のように、「水蒸気は水素原子と酸素原子が1；1で結びついた複合原子である」と考えると、

図のように、2：1：2となるためには、酸素原子が反応後に増えることになり、原子説の(4) 化学変化では、原子と原子の結合の仕方が変わるだけで、原子自身が新たに生成したり、消滅したりすることはないということに矛盾します。また、原子の数を合わせるなら酸素が2原子あればいいことになりますが、その場合は体積比が2：2：2＝1：1：1となり、気体反応の法則が成り立たないことになります。

(ⅲ) さらに、下図のように、「水蒸気は水素原子と酸素原子が2；1で結びついた複合原子である」と考えると、

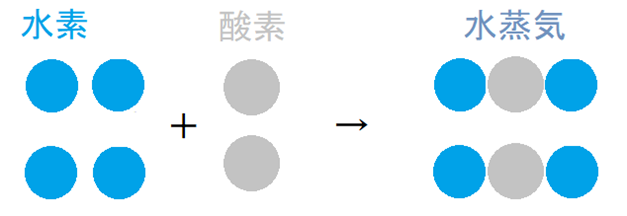
図のように、原子の数が合っていても、体積比が4：2：2＝2：1：1となってしまい、気体反応の法則が成り立たないことになります。

このように、どう説明しようにも上手くいかなかったのです。
（特に、(ⅰ)の矛盾点は実際に入試で説明させられる問題もあるため、しっかりと理解しておきましょう）

この気体反応の法則を上手く説明し、当時信じられていた原子説の矛盾点を解決するため、新たに発表されたのが「分子説」です。

６．分子説

1811年に、イタリアの科学者アボガドロが発表しました。

以上の2つのルールが分子説とよばれるものです。

この分子説に従って、水素は水素原子2個からなる分子、酸素は酸素原子2個からなる分子、そして水蒸気は水素原子2個と酸素原子1個からなる分子であると考えて、先程の気体反応の法則を説明すると、

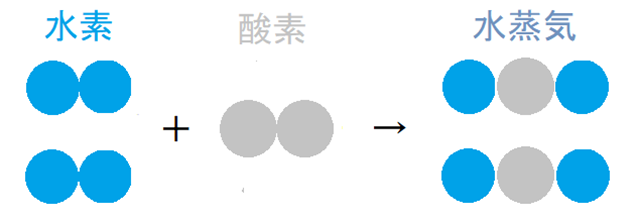
図のように、気体反応の法則を矛盾なく説明することができます。

こうして、原子という粒子の他に、「分子」という粒子を考えることで、上手く説明することに成功しましたが、実験的な検証が出来なかったこと、原子同士が結合して分子を作る際の結合のしくみが解明されておらず、当時はこの分子説は受け入れられず、認められるまで約50年かかりました。

今では、この(2)の法則をアボガドロの法則と呼んでいます。

ここで注意ですが、
化学の問題でも使うことの多い「アボガドロ定数」は、もちろんこの(2)のアボガドロの法則と関わりのある内容ですが、アボガドロ定数が具体的に求められたのは分子説の発表からずっと先のことであり、アボガドロ自身が求めた値ではありません。誤解のないようにしておきましょう。

まとめ

いかがだったでしょうか。

分量も多く、思った以上に複雑なので、敬遠しがちな内容ですが、この機会にきちんと学習しておきましょう。