受験化学の計算問題における数値の取り扱い方（前編）

京都医塾化学科の児玉です。

化学の計算問題において、「有効数字〇桁で答えなさい。」という問題をよく見ると思います。

正しく計算して答えを書いたにもかかわらず、有効数字が違っていたために減点された、なんてことも皆さん経験があることでしょう。

そこで、化学の計算問題においての、数値の取り扱い方を教えたいと思います。

まずこの記事では有効数字について考えてみましょう。

まず、有効数字とは？？

有効数字とは、「有効」な「数字」と考えれば理解しやすく、簡単に言うと「意味のある数字」のことです。

図で示された状況を考えましょう。

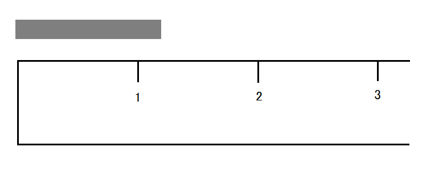
最小の目盛りが1cmの定規でものの長さを測っています。

図を見て、皆さんはこの長さを何cmと判断しますか？

1cm～2cmの間を大体の目分量で測って、1.2cmくらいかな…？と考える人が多いと思います。

このように、何かを測定するときには測定値の限界というものが存在します。この図を見て、「1.2cmじゃない、1.23cmだ」と言われても、0.03cmの差は目分量では分かりませんよね。

先ほど説明した「意味のある数字」は1.2までで、0.03は「意味のない数字」と考えると、有効数字の考え方がより分かりやすくなるかと思います。

では、例を使って有効数字の桁数を考えてみます。

まずは、1.2という数字を考えてみましょう。

この1.2という数字は、1.15を四捨五入して得られた、と考えることもできますし、1.24を四捨五入して得られた、と考えることもできます。

つまり、1.2という数字だけ見ても、正確に見ると1.15～1.24という幅が存在するのです。

もちろん、「1.2〇〇」の〇に当てはまる3桁目以降はどんな数字なのかは分からないため、3桁目以降は「意味のない数字」であり、2桁目までの1.2は「意味のある数字」と言えます。このことから、1.2は有効数字2桁と表現するのです。

これが有効数字の基本です。

次に、「0」という数字はどう扱うのかを説明します。

例えば、1.20という数字を考えます。

同じように考えると、1.20という数字は、1.195～1.204という幅が存在することになります。

ここでは、「1.20〇〇」の〇に当てはまる4桁目以降は「意味のない数字」となり、3桁目までの1.20は「意味のある数字」と言えるので、1.20は有効数字3桁と表現します。

それ以外の例として、0.012という数字を考えてみましょう。

この0.012という数字には、0.0115～0.0124という幅が存在するということは、今までと同じように考えれば分かりますね。

この場合、「意味のある数字」は「1」と「2」であり、最初の0は「意味のない数字」です。（位取りと言います）

つまり、0.012は有効数字2桁と表現します。

そして最後に、1200という数字を考えてみます。

この数字には注意が必要で、

というように、四捨五入する位に3つの可能性が考えられます。

有効数字が何桁なのかが分からないのです。

このような場合は、指数表記（〇×10^□）で表すのが普通です。このとき、〇に当てはまる数字は、1≦〇＜10の範囲の数字を用いて表します。

今回の1200という数字で考えると、「1.2×10³」（有効数字2桁）と表すのです。

有効数字3桁で表したい場合は、「0」の数字の扱い方で示したように、「1.20×10³」と表せばよいことになります。

有効数字とは、「意味のある数字」のこと。 0については、最初にある0（位取りの0）は有効数字にはカウントしない。後ろにある0は有効数字としてカウントするが、「1200」のように整数で表したときの0は有効数字が分からなくなるので、指数表記（〇×10□）で表し、〇の部分で有効数字を表す。

以上、有効数字についての説明でした。

後編では、途中計算における有効数字についての注意事項について説明しようとおもいます。