京都医塾化学科の児玉です。
前回の記事では、「有効数字とは何か」についてを説明しました。
まだ、読んでいない方は下記の記事を先に読んでください。
今回は、有効数字が関わってくる計算についての注意点を説明したいと思います。
有効数字が関わってくる計算についての注意点
次のような例題を考えてみましょう。
21gの塩素(Cl2:分子量71)がある。以下の問いに有効数字2桁で答えよ。
(1) 塩素の物質量(mol)を求めよ。 (2) 塩素の標準状態での体積(L)を求めよ。
まずは(1)です。
質量(g)から物質量(mol)に変換するためには、質量を分子量で割ればいいので、塩素の物質量は、
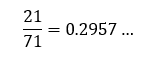
と計算でき、有効数字2桁ということから、3桁目の「5」を四捨五入して、答えは0.30molとなります。
よくある、一般的な計算問題ですね。
注意が必要となるのは、(2)です。まず、間違っている回答を記します。
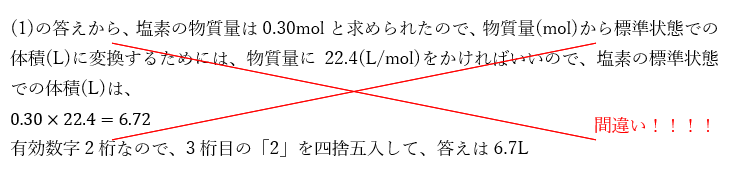
この解答、正しく解答出来ているように見えますが…、どの部分が間違っているか皆さんは分かりますか?
間違いのポイントは、(1)で求めた物質量を0.30molとして計算してしまっていることです。
(1)の解答に記したように、実際の値は0.2957…となっているところを、3桁目を四捨五入したものが、0.30molという解答です。
このことから、(1)の最終的な答えとして出した0.30という値は少しズレがあり、その値を用いて求めた6.72Lという答えにも当然ズレがあることになります。
このように、途中計算に用いる値は、示された有効数字で表した値を用いるのではなく、有効数字の桁数より1桁多い値(以降の値は四捨五入ではなく切り捨て)を使って計算しなければなりません。
今回では、物質量は正確には0.2957…という数字であり、有効数字2桁で答えよという問題のため、途中計算は有効数字3桁目までの数値を使う必要があります。4桁目以降は切り捨てとするのが基本のため、使用する物質量の値は0.295molです。
この値を使ってもう一度答えを求めてみましょう。
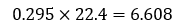
有効数字2桁なので、3桁目の「0」を四捨五入して、答えは6.6L
初めに記した値と異なる値が出てきましたが、もちろん正確な値は後者の6.6Lです。
この例題のように、示された有効数字で答えを出した問題では、途中計算で用いる値に注意を払わなければ、最終的な答えが間違った値で出てくることがあるのです。
ただ、ここまで読んでもらった人の中には、「桁数を1つ増やして計算すると、計算量が多くなって計算ミスしてしまいそう…」と感じる人もいるでしょう。
特に、有効数字3桁で答えなければならない問題では、途中計算で用いる値は4桁目まで使うこととなり、計算量が格段に多くなるのは確実です。
この場合、最も正確で、かつ効率よく計算するのは、最初の計算で出てきた分数をそのまま利用することです。
今回の問題で例えると、物質量の計算では21/71を計算していました。そこで、この分数をそのまま(2)でも使うのです。つまり、
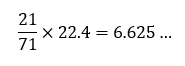
と計算し、有効数字2桁なので、3桁目の「2」を四捨五入して、答えは6.6L
このようにすると、計算量をあまり増やさないまま、正確な値が得られます。
まとめ
今回の内容をまとめると、有効数字で表すために四捨五入した値は、ズレがあるため、示された有効数字で表した値を途中計算で用いると、最終的な値もズレてしまい、解答と異なる値を計算してしまう。
このズレをなくすためには、有効数字の桁数より1桁多い値(以降の値は四捨五入ではなく切り捨て)を用いて計算しなければならない。その他、安全かつ確実な方法は、最初の計算で出てきた分数をそのまま利用すること。
有効数字についてはあまり細かく扱ってもらえず、曖昧なまま使っている受験生も多いことでしょう。しかし、これらの記事を通して、有効数字についての考え方が身についたかと思います。今後、有効数字で減点されることの無いように、2つの記事での内容を念頭において、計算問題に挑戦してみてください。
京都医塾ではご相談・体験授業を随時募集しています。下記リンクからお気軽にお問い合わせください。


_アートボード-1.png)
