京都医塾 数学科の山本です。
先日生徒に過去問指導をしているとき、
生徒によっては中学内容の知識をパッと使えないことがあるなあ、と感じる場面がありました。
例えば、「底辺が共通な2つの三角形の面積の比は、高さの比に等しい」というものです。ベクトルなどの図形問題の小問で面積をきかれているときに使えると、計算量を少なくできることが多いので便利な知識ですね。
どういうものか、一応確認しておきましょう。
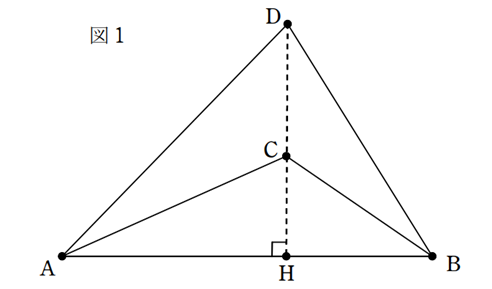
図1において、△ABCの面積をS1、△ABDの面積をS2とすると、S1:S2=CH:DHというものです。
これ自体なら一目見て使えるぞと気づくのですが、これに相似が絡んだ形で出題されると、気付きにくいようです。
例えば2019年度川崎医科大学の問題をみると、

△ABDは正三角形で、四角形ABCDは円に内接しており、BE:EDは1:2。
また、(1)でAB=1、(2)でAE=\(\frac{7}{9}\)
を求めている。
このような図形(実際の問題には図は描かれておらず、自分で図を描いて考える必要があります)において、(4)で、正三角形ABDの面積を求めたうえで、四角形ABCDの面積を求めることを要求されています。△ABDは求めているので、△CBDを求めれば四角形ABCDの面積を求めることができますね。
ここで、辺BCや辺CDの長さを求めて、三角比を使った面積の公式を使って計算するのは、とても面倒な予感がします。
ここで、△ABDと△CBDは辺BDを共有しているので、辺BDを底辺として、先ほどの「底辺が共通な2つの三角形の面積の比は、高さの比に等しい」を使えば、計算が楽になりそうです。ここで、次の図3のように、それぞれの三角形に高さATとCSをかきこんでみましょう。
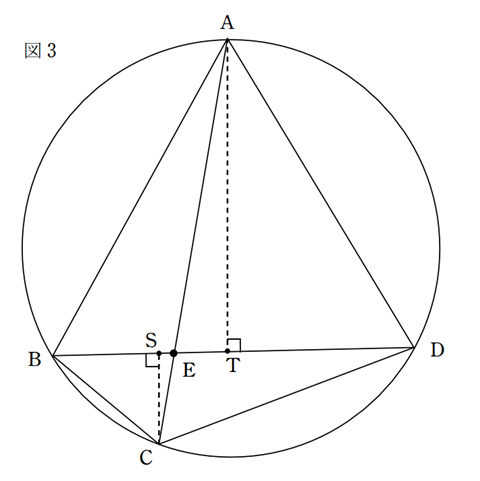
このとき、△AETと△CESは相似なので、AT:CS=AE:CEとなります。
なので、AE:CEを求めることができれば、△ABDと△CBDの比を求める(ひいては、△CBDの面積を求める)ことができますね。
方べきの定理より、AE×CE=BE×DEという式を立てられるので、後は計算でCEを求めることができます。
(実際の問題はベクトルの問題だったので、誘導に乗ってベクトルの計算で処理した受験生が多かったと思います)
このように、上手く比を利用すると計算量を減らす(あるいは、複雑な計算を避ける)ことができるので、中学範囲の知識も疎かにしないようにしましょう。


