皆さんこんにちは。京都医塾数学科講師の田村がお送りいたします。

　受験数学の最頻出問題といえば、なんといっても「微分法・積分法」ですね。微分法を用いて接線の傾きを求める、積分法を用いて面積や体積を求めるといったことは、受験生の皆さんにとっては日常茶飯事だと思います。

　普段何気なく使っている微分と積分ですが、少し考えてみると、接線の傾きを求める演算である微分法と面積を求める演算である積分法が足し算と引き算のような逆の関係にあるのは少し不思議な気がしますね。そもそも、「なぜ定積分の計算で曲線が囲む面積が求まるのか」ということも、きちんと答えようとすると難しそうですね。

　ということで今回は、定積分計算と面積の関係についてお話していきたいと思います。加えて、この話にかかわった有名な数学者についてもご紹介していきます。

定積分で面積が求まる理由

設定

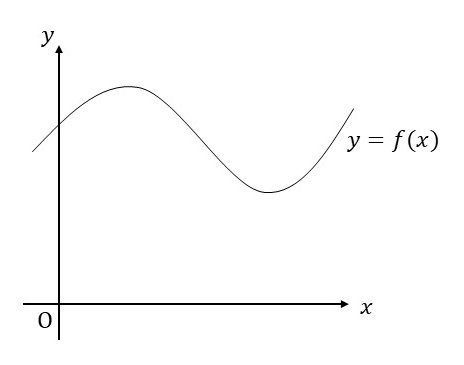
まず、関数 \(y=f(x)\) を用意しましょう。

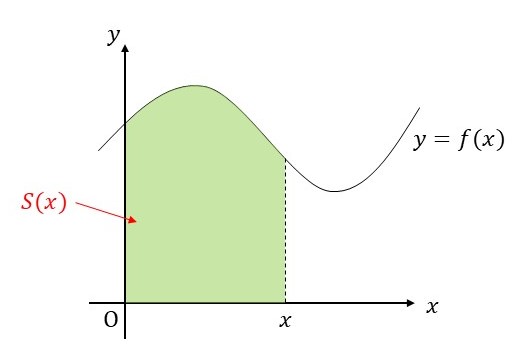
そして、関数 \(S(x)\) を「\([0,x]\) の範囲で \(y=f(x)\) と \(x\) 軸とで囲まれる部分の面積」を表す関数とします。下図の緑色の部分の面積を \(S(x)\) とする、ということですね。

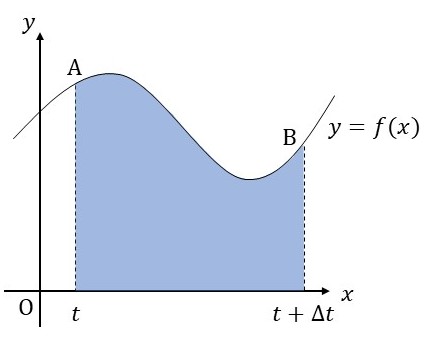
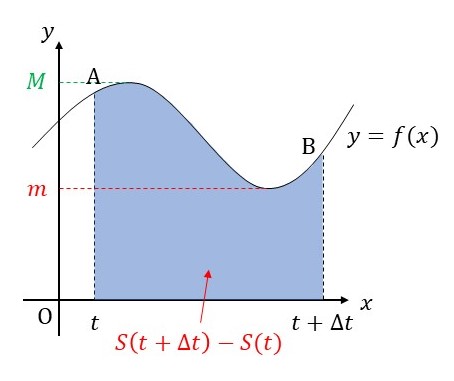
　では、この関数を用いて下図の青色の部分の面積を求めてみましょう。

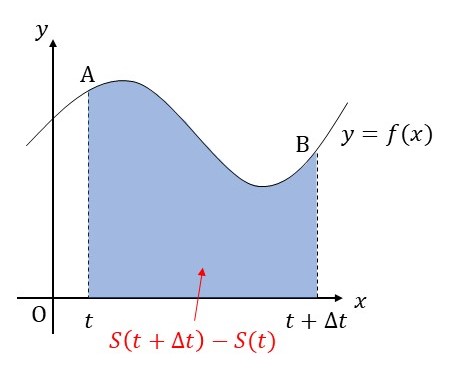
この部分の面積を \(S(x)\) で表すとどうなるでしょうか？ \([0,t+\Delta t]\) の部分から \([0,t]\) の部分を引いているので、面積は \(S(t+\Delta t)-S(t)\) となります。

　最後に、とても重要な設定をします。区間 \([t,t+\Delta t]\) における \(f(x)\) の最大値を \(M\)、最小値を \(m\) とします。

なぜこんなことをするのかわからないと思いますが、今は「ふーん」ぐらいに思っていただければ大丈夫です。

　これですべての設定が終わったので、実際の議論に入っていきましょう。

本論

　曲線で囲まれる面積 \(S(t+\Delta t)-S(t)\)は、下図の2つの長方形の面積で挟み込むことができます。

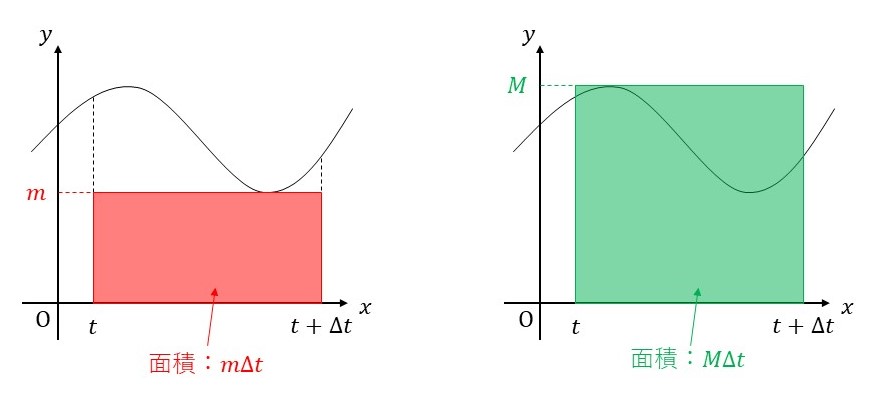
つまり、\(m \Delta t≦S(t+\Delta t)-S(t)≦M \Delta t\)という式が成り立ちます。この式の各辺を \(\Delta t\) で割ると、

\(\displaystyle m ≦\frac{S(t+\Delta t)-S(t)}{\Delta t}≦M　\cdots①\)

となります。この式において、「長方形の横幅を限りなく小さくしていくとどういうことが起こるのか」ということを考えてみましょう。つまり、\(\Delta t \to 0\) での極限を考えるということですね。このとき、点 \(B\) は点 \(A\) に近づいていくため、最大値も最小値も \(f(t)\) に近づきます。

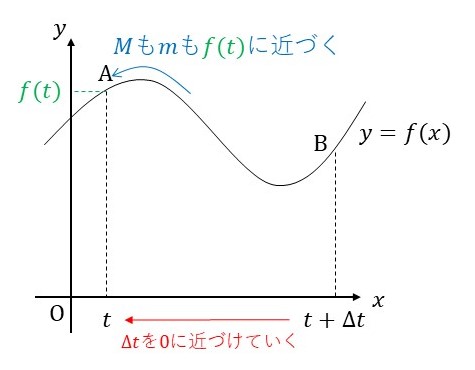
つまり、\(\displaystyle \lim_{\Delta t \to 0}m=\lim_{\Delta t \to 0}M=f(t)\) が成り立ちます。①の最左辺と最右辺がともに \(f(t)\) に収束するので、はさみうちの原理より

\(\displaystyle \lim_{\Delta t \to 0}\frac{S(t+\Delta t)-S(t)}{\Delta t}=f(t)　\cdots②\)

が得られます。この式の左辺、どこかで見覚えがないでしょうか？これは「微分係数の定義」の形ですね。

\(\displaystyle f'(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}\)

これにより、②式は \(S'(t)=f(t)\) と変形できます。この式は、「面積を微分すると関数値になる　\(\Rightarrow\)　関数を積分すると面積が求まる」ことを表しています。

　この事実を「微分積分学の基本定理」といいます。それぞれ独立のものと認識されていた微分法と積分法が実は逆の関係にあることを示した、当時の常識を覆すような定理となっています。

微分積分学の基本定理を導いた人たち

　では、この定理の導出にかかわった人たちを紹介していきます。

アイザック・ニュートン

　万有引力でおなじみのニュートン。実は、この微分積分学の基本定理を最初に導いた人であることが知られています。ニュートンは1665年ごろに定理を導いたと言われています。また、ニュートンは微分の記法として \(\dot{x}\) というものを作りました。あまりなじみのない記号かもしれませんが、これは物理学でよく使われる記号です。大学で力学を学ぶときに目にすることになると思います。

ゴットフリート・ライプニッツ

　定理を導いたと言われているもう一人がライプニッツです。ライプニッツがこの定理を導いたのは1675年ごろと言われていますが、ニュートンよりも先に世間に公表したことから、ニュートンとどっちが先かで一悶着あったようです。どちらかが剽窃したという事実はなく、各々が独立に定理を導いたと言われています。ライプニッツは微分の記号として \(\displaystyle \frac{dy}{dx}\) というものを作りました。

　また、定理の成立とは特に関係のない人物ではありますが、皆さんが良く使う \(y’,f'(x)\) の記号はジョゼフ＝ルイ・ラグランジュという数学者によって作られました。

まとめ

　当たり前のように使っている微分法・積分法ですが、裏にはこういった理論が隠れています。もちろん、この「微分積分学の基本定理」を知っていないと解けない問題は入試ではまず出題されることはありませんが、教養の一つとして頭の片隅に置いておいていただければ幸いです。これからも楽しく数学を学んでいきましょう！