京都医塾生物科の井崎です。この記事は、＜酸素解離度の公式＞の第2回です（全3回）。第1回の記事をまだ読んでいない方は、そちらを先に読まれることをお勧めします。

まず、＜酸素解離度の公式＞を再確認しておきましょう。

ですね。「酸素ヘモグロビンの割合」は、肺では約95％、組織では約30％だとしましょう。

すると、分母は95(%)になり、100(%)にはなりません。100(%)なら計算が楽だったのにね。「なぜ、こんなに計算が面倒な公式になっているのでしょうか？」、そこを考えてみましょう。

例えとして、「タクシー会社の乗客輸送効率」というものを考えてみましょう。下図を見て下さい。この会社のタクシー100台が町中をグルグル回って、客を乗せたり降ろしたりしている、とします。

そして、100台のタクシーは、駅前で95台が客を乗せ、オリンピック会場で65台が客を降ろした(つまり差分の30台の客には別の行先があって、オリンピック会場では降りなかった)、としましょう。また、残り5台のタクシーは駅で客を拾えず、空車で町中をグルグルと回っています。

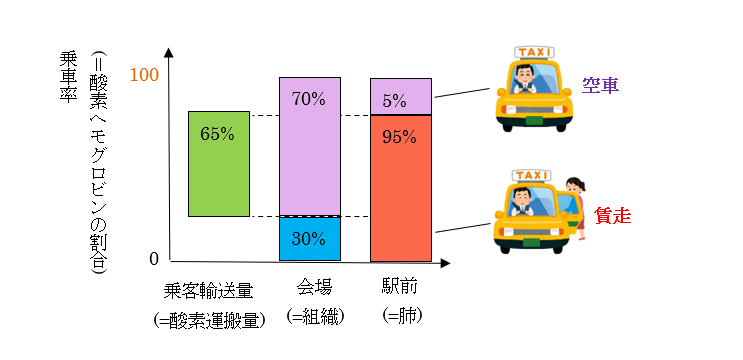
ここで、「駅前からオリンピック会場までの乗客輸送効率」というものを、2通り考えてみることができます。

違いは、「常に空車で町中をグルグルと回っている5台のタクシー」を分母に算入するかしないか、だけです。そして「この空車の5台のタクシー」は、何も仕事をしていないようにも見えるのです。輸送効率の表現方法に上記の二通りがある時、どちらの方が「数値の見かけ上、効率が良いかのように見える」でしょうか？

①式の発想は、このタクシー会社の例で擬人的に言えば、「5台のタクシーは客を乗せもせずにずブラブラ遊んでいるようなものだから、輸送効率の計算に入れてあげない」という、「世知辛い発想」です。この場合、輸送効率＝約68.4(%)と、②式より少し高く数値が出ます。タクシー会社がオリンピック関連で「仕事やってます感」を数値的に盛りたければ、こちらを使うべきでしょう。

②式の発想は、「タクシーやってりゃ客を拾えない日もあるさ、それでも私達の仲間だから、5台のタクシーも計算に入れてやろうぜ」という、「共同体主義的な発想」です。この場合、輸送効率=65(%)となり、先の①式よりも「見かけ上」は数値が少し下がります。 医学で使われる「酸素解離曲線」の発想は、①式のそれです。何故、②式ではなく①式を使うのでしょうか？　次回の記事では、その点を考えていきましょう。