京都医塾数学科です。

このページでは「金沢医科大学医学部の数学」についての過去問分析コメントを紹介します。
・“医学部受験に興味がある”という方
・“金沢医科大学医学部”の受験を考えている方
・“金沢医科大学医学部の数学がどのような問題か知りたい”という方
におススメの記事となりますので、興味のある方はご一読ください。

概要

【形式・制限時間・配点】2022年度（最新の問題より）

形式： 全4問、全てマーク式
制限時間：60分
配点：100点（一次試験の総得点は350点）

出題の傾向と特徴

形式に加え、大問数が4問に固定されてきた2016年度以降の傾向について、まとめます。

【恒例の出題単元】

7年連続で、第1問にサイコロを用いた確率の問題が出題されています。
図形や方程式・不等式といった数学Ⅰの他分野との混合で出題されることもあります。
場合の数・確率の最も重要な（そして軽視されがちな）考え方である「数え上げ」を意識させるような問題が多く、他大学の入試でよく出題されるような反復試行・条件付き確率・確率漸化式と言った問題は、全く出題されていません。
樹形図や表を用いて、数え漏れが無いように丁寧に数え上げる練習を積んでおきましょう。

また、「微分・積分」の問題も、毎年のように出題されています。
数学Ⅲ範囲の出題が多いですが、最新年度も含め、数学Ⅱ範囲からの出題も少なくありません。
面積・体積を求める典型問題が出題されており、難問はありません。
教科書の練習問題レベルが正確に、かつ短時間で解き切れるように、演習を積んでおきましょう。

【頻出の出題単元】

4つの大問で、各分野からバランスよく出題されています。
【恒例の出題単元】でも書いた通り、数学Aから確率（三角比・二次不等式といった数学Ⅰとの混合で出題されている事も多い）、数学Ⅲ（もしくはⅡ）から微積分の2問が固定されており、残りは数学B、数学Ⅱ（もしくはⅢ）から1題ずつ出題されています。

数学Bからは、数列・ベクトルのいずれかが毎年出題されています。
いずれの単元も、教科書レベルの基本知識を丁寧に身に付けることが重要です。
焦って難しい問題集に手を出す必要はありせん。

【制限時間に対する問題量】

60分で大問が4つですから、マークする時間や見直しを引くと、1問当たりにかけられる時間は10分強です。
計算にかかりきりになって、「気付けば1問に20分以上かけてしまった」という事が無いように、時間配分には十分注意しましょう。
また、計算速度の向上はもちろん、より効率的な解法を選択することを心掛けましょう。

2022年度（最新の過去問）の分析

ここまでは近年の傾向を見てきましたが、ここではさらに踏み込んで、最新の入試問題を具体的に分析したいと思います。
※2022年度から前期入試が2日間ありますが、ここでは赤本に掲載されている1日分のみ扱う事とします。
※以下、過去問をお手元にご覧になるのが理想的ですが、過去問がなくても問題なくお読み頂けます。

【第１問　確率】（難易度：標準）

サイコロを3個投げて、出た目( \(a,b,c\) )を代入する事によって作られる値( \(\frac{3^{a}-2^{b}}{5^{c}}\) )について考察します。
この大学の定番の出題形式であり、スマートな解法は特にありませんので、丁寧に調べ上げることが求められます。
時間さえあれば最後まで解ききることはできますが、他の問題にかけられる時間との相談になります。

(1)のポイント： \(p\) の符号を調べるには、分子( \(3^{a}-2^{b}\) )のみに着目すればよいと分かります。
分母は1～6の任意の数を取ることが出来るので、分子の場合の数に6通りをかける事（積の法則）を忘れないようにしましょう。

なお、ここでサイコロ2個で作られる分子の \(6^{2}=36\) 通りを、以下のような表を埋める事で全てのパターンを調べておけば、(2)以降の考察が一気に楽になります。

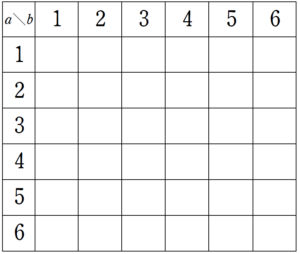
(2)のポイント： \(p\) が整数になるためには、分子が 5 の倍数である必要がある。
最大もしくは最小の整数になるのは \(c=1\) である事に気付けば、あとは(1)で作成した表を用いて分子が最大・最小になる時を調べるだけです。

(3)のポイント：(2)と同様に、(1)で作った表を用いて該当する \((a,b)\) の組を調べればよいでしょう。
分子が 25 の倍数であれば \(c\) が1,2を取れる事に注意しましょう。

(4)のポイント：立てた不等式について、 \(c\) の値によって場合分けしながら、やはり(1)で作った表を参照して数え上げます。例えば、 \(c=1\) の場合は、(分子) \(<45\) となり、(1)で作った表を基に数え上げます。
※余事象、つまり \(p≧9\) の場合を考えた方が効率的になります。

≪2022年度の目標値≫
数学を得点源にしたい受験生…他の大問を効率的に解き、多少時間を費やしてでも完答。
他教科を得点源にしたい受験生…まずは(2)までを解きたい。残りは時間と相談。

【第２問　微積分（数学Ⅱ）】（難易度：やや易）

3次曲線とその接線のもう一つの交点、その2つの図形で囲まれる部分の面積を計算する問題です。
他の大学でも出題されやすい超典型問題ですが、この大学では「微積分」は数学Ⅲを中心に出題されていたため、このタイプの問題に慣れていない受験生もいたでしょう。

・「2つのグラフが接する」→「方程式が重解を持つ」の言い換え
・3次曲線と接線で囲まれる面積についての「 \(\frac{1}{12}\) 公式」… \(\int_{α}^{β}a(x-α)(x-β)^{2}dx=\frac{a}{12}(β-α)^{4}\)
以上の2点を活用できたかどうかで、計算にかかる時間に大きな差が付きます。
（前者の知識は3回、後者は2回用いることになります。）

また、3次曲線の性質の1つ、「変曲点で点対称」を利用することが出来れば、更に計算を簡略化できる余地があります。

空欄ヘホのポイント：四角形 \(PQRS\) が「1組の対辺が平行」・「点対称」より平行四辺形である事が分かれば、対角線（ \(PR\) もしくは \(QS\) ）で分割した三角形の面積を2倍すればよい事が分かります。

≪2022年度の目標値≫
数学を得点源にしたい受験生…上記の知識を用いて、素早く完答。
他教科を得点源にしたい受験生…完答。（4と比較して解きやすい方を優先。）

【第３問　ベクトル】（難易度：(1)～(3)は易、(4)は標準）

座標空間上にて、1点からある平面（特定の3点を通る）に向けて下した垂線と平面の交点を考えることで四面体の高さを計り、最終的には2つの四面体の体積比を考察する問題です。

「平面に下した垂線」は教科書レベルの典型問題です。
・始点(D)と基準となるベクトル( \(\overrightarrow{DA}\) , \(\overrightarrow{DB}\) , \(\overrightarrow{DC}\) )を定める…(1)の空欄の形に合わせて定めればよいだけ
・「4点 \(A,B,C,P\) が同一平面上に存在する条件」（共面条件）… \(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\)　( ただし \(s+t+u=1\) )
・「直線と平面の垂直条件」…平面上にある2つのベクトルと垂直（→内積が0になる）

以上の知識を正しく運用出来れば、(3)までは比較的短時間で解き進めることができます。

(1)のポイント：上記3点の知識を活用し、各ベクトルの係数についての連立方程式を立てる。
空欄の形（ \(\overrightarrow{DA}\) と \(\overrightarrow{DC}\) の係数が一致する ）から文字を1つ消去することが出来るので、計算量を減らすことができます。

(2)・(3)に関しては、(1)の計算結果を活用すればすぐに求めることが出来ます。

(4)のポイント：2つの四面体は共通の高さ（ \(DH\) ）を持つため、( 体積比 ) = ( 底面積の比 ) と読み替えることが出来ます。
2直線の交点を求めるため、「3点が同一直線上に存在する条件」（共線条件）を用いて連立方程式を立てる必要があります。
(3)までの計算に手間取って時間を費やすと、この問題に取り組むことは困難でしょう。

≪2022年度の目標値≫
数学を得点源にしたい受験生…(3)までは確保、(4)は残り時間次第。
他教科を得点源にしたい受験生…(3)まで。

【第４問　二次曲線・微積分（数学Ⅲ）】（難易度：やや易）

ともに原点を頂点とする、2つの放物線
\(y=2x^{2}\) ……①（下に凸）
\(y^{2}=4t^{3}x\) ……②（左に凸）
の交点や接線、囲まれる部分の面積・体積を求める問題です。
全体として教科書練習問題レベルの設問であり、最後の面積・体積の定積分を利用した計算についても複雑ではありません。

空欄ワ～あについては、微分係数を利用して接線の方程式を求めるだけの基本問題です。

空欄い・うのポイント：横の放物線の接線は、
・「両辺を \(x\) で微分」… \((y^{2})’=2y・y’\) （合成関数の微分）に注意
・接線の公式利用… \(y_{1}y=2p(x+x_{1})\)　（接点の座標が \((x_{1} , y_{1})\) ）
以上のいずれかを利用して求めます。
また、2直線のなす角は（傾き）=（ \(x\) 軸の正の向きとのなす角の \(\tan\) ）であることを利用します。

空欄え～きのポイント：「分数関数の最大値」→「導関数から増減を考察」とすると、大幅にタイムロスです。
分母・分子を \(t\) で割ると、分母に相加平均・相乗平均の大小関係を適用できます。（ 条件 \(t\gt0\) がヒント ）

空欄く～このポイント：2つの放物線が「逆関数」（ \(x↔y\) の関係 ）にある事から、①の放物線と対称軸 \(y=x\) で囲まれる部分の面積を2倍すれば、いわゆる「 \(\frac{1}{6}\) 公式 」を活用して効率的に計算できます。

空欄さ～すのポイント：2つの曲線で囲まれる部分の回転体の体積は、「引いて2乗」では無く「2乗して引く」。
曲線と \(x\) 軸で囲まれる部分の回転体の体積は\( \int_{a}^{b}y^{2}dx \) で計算するので、放物線②を \(y=\)～ と変形する必要はありません。

≪2022年度の目標値≫
数学を得点源にしたい受験生…完答。
他教科を得点源にしたい受験生…完答。（2と比較して解きやすい方を優先。）

【総評】

積分を利用した面積・体積を求める問題が2問出題されているので、計算に手間取ってしまうと時間不足に悩まされる事になります。
しかし、いずれも「超」が付くほどの典型問題ですから、基礎～標準レベルの問題演習を積んで、素早く計算できるようにしておきましょう。

まとめ

最近7年間を見ても傾向がほとんど変わっていないので、対策は立てやすい大学です。
問題の難易度自体は私立医学部の入試問題の中でもかなり簡単な部類に入りますが、忙しい試験になる事は間違いありません。
過去問演習を通じて、「60分で4問」の時間配分に慣れておきましょう。
また、素早く答えを出す事を意識して演習に取り組みましょう。

京都医塾ではご相談・体験授業を随時募集しています。下記リンクからお気軽にお問い合わせください。