突然ですが問題です。

問題

次の実数 \(x\) についての命題は真か偽か。

「 \(x^2 <0\) ならば \(x=0\) 」

解答

答えは真です。

意外に思った方も多いかもしれません。

なぜならば \(x^2<0\) となるような実数 \(x\) など存在するはずもなく、でたらめなことを言っているように聞こえるからです。

しかし、その反論はあくまで「 \(x=0\) ならば \(x^2 <0\) 」が偽であることを述べたにすぎません。

実は前提条件を満たすものが存在しなければ全体の命題は必ず真となります。

「集合」を利用して納得

とはいえ、直感から反するように感じるのも無理はありません。

今回は納得する方法を2つ紹介したいと思います。

手始めに次の命題を考えます。

「\(x\) が \(3\) 以上の素数ならば \(x\) は奇数である」

3以上の素数からなる集合を \(\textrm{Q} \)

奇数からなる集合を \(\textrm{P} \)

とします。

これらの集合を「ベン図」で図示してみます。

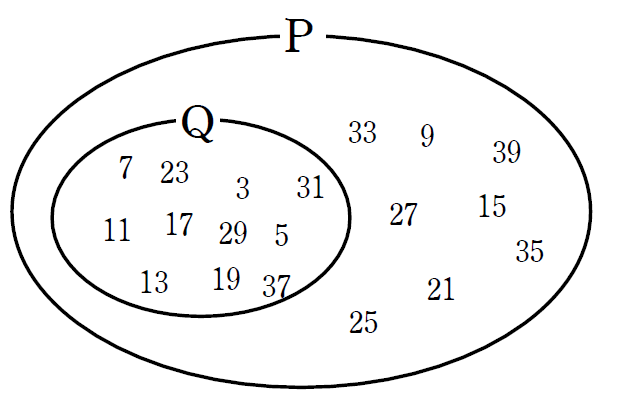
ベン図から読み取れるように \(\textrm{Q} \) は \(\textrm{P} \) の部分集合となります。

つまり \(\textrm{Q} \) に含まれる数はすべて \(\textrm{P} \) に含まれます。

「3以上の素数」はすべて「奇数」ということが視覚的に確認できました。

したがって「\(x\) が \(3\) 以上の素数ならば \(x\) は奇数である」は真となります。

それでは問題に戻りましょう。

「\( x^{2} < 0 \) を満たす実数 \(x\) 」からなる集合を \(\textrm{Q} \)

「\(x=0\) を満たす実数 \(x\) 」からなる集合を \(\textrm{P} \)

とします。

当然ながら \(\textrm{Q} \) に含まれる数はありませんし、 \(\textrm{P} \) に含まれる数は \(0\) だけです。

さて、この結果をベン図に図示するとどのようになるでしょうか。

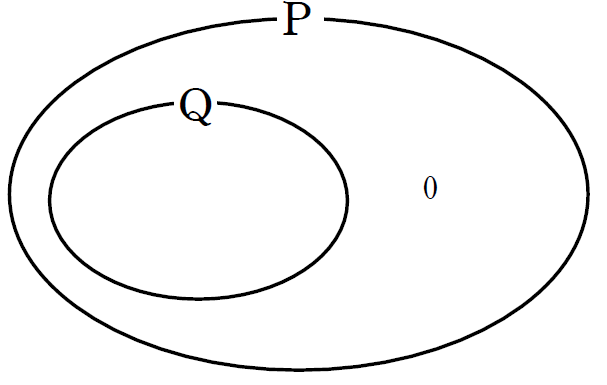
やや寂しいベン図になってしまいました。

\(\textrm{Q} \) に含まれる数はありませんから、まるで空っぽの袋のようになっています(このような集合のことを空集合と呼びます)。

しかし、図のように \(\textrm{P} \) の中にすっぽり入れることは可能です。

「空集合は任意の集合の部分集合になっている」と言い換えることもできますね。

結果的に先ほどの例と同じく \(\textrm{Q} \) は \(\textrm{P} \) の部分集合となります。

したがって同じように「 \(x^2 <0\) ならば \(x=0\) 」が真と言えます。

「対偶」を利用して納得

先ほどの「集合」の例は少し騙されたような印象を受けた方もいるかもしれません。そこで別の考え方も紹介します。

さて、無理数が「有理数でない実数」と定義されるように、虚数が「実数でない複素数」と定義されるように、「否定」により定義されるものを否定してみます。

「無理数でない実数」は有理数ですし、「虚数でない複素数」は実数になります。

そのため「否定」により定義されるものは、さらに「否定」すると扱いやすくなります。

たとえば \( \sqrt{2} \) が無理数であることの証明で背理法を用いますが、結論を否定して\( \sqrt{2}\) を有理数と仮定することで「 \( \displaystyle \sqrt{2}=\frac{m}{n} \) ( \(m,n\) は正の整数) 」と表現できます。無理数よりも有理数の方が整数を用いた直接的な表現ができるため、論証に使いやすいわけです。

今回も \(x^{2}<0\) となる実数 \(x\) は存在しないため、「否定」が有効かもしれません。

さて、背理法と同様に「否定」を用いるものといえば「対偶」です。

そこで、今回は問題の命題の対偶を考えてみます。

実数 \(x\) についての命題で

「 \(x^2 <0\) ならば \(x=0\) 」

の対偶は以下のようになります。

「\(x\ne 0\) ならば \(x^2 ≧0\)」

この命題は真でしょうか。偽でしょうか。

\(x\) に \(0\) 以外の値を色々代入してみましょう。

どのような値を代入しても \(x^2\) は \(0\) 以上の値になります。

こちらは最初の命題と比べて自信を持って真と答えられるはずです。

命題の対偶が真であれば元の命題も真ですから、解答にも納得ができますね。

まとめ

今回は「前提条件を満たすものが存在しない命題」というイレギュラーな問題を扱いました。

しかし、「集合」を用いる解法も「対偶」を用いる解法も集合と命題の単元において非常にオーソドックスな解法です。特に共通テストを受験する方にとっては是非とも習得したいテクニックです。

様々な問題でこれらの解法を活用してみてはいかがでしょう。

それでは最後までお読みいただきありがとうございました。