京都医塾数学科のふくいです。

順天堂大学医学部の2021年度一般入学試験(1次試験)で以下の問題が出題されました。

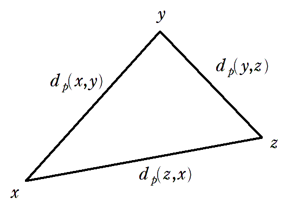
ある素数 \(p\) および互いに異なる整数 \(x，y\) に対して\(p^{n}\) が \(x-y\) を割り切るような整数 \(n\) のうちで最大のものを \(n_{p}(x-y)\) と表し，\(d_{p}(x,y)=p^{-n_p (x-y) }\) と定義する。また，\(d_{p} (x,x)=0\) とする。

(中略)

(3)　すべての整数 \(x,y,z\) について \(d_{p} (x,z) ≦ d_{p} (x,y)+d_{p} (y,z)\) が成り立つことを示せ。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

順天堂大学医学部2021年度一般入学試験第3問より抜粋

今回は上記の問題の(3)を題材に，複数の単元に登場する「三角不等式」を紹介したいと思います。

そもそも \(d_{p}\) の \(d\) って何？

\(d\) は「距離」を表す英単語 distance の頭文字です。先述の順天堂大学医学部の問題は，実は大学の数学科で学ぶ「代数幾何学」をはじめとする数学の諸分野に登場する「\(p\) 進距離」と呼ばれるもので，
2整数の距離を「2整数の差が素数 \(p\) で何回割り切れるか」をもとに定義したものになります。

入試問題としては，(3)は証明問題の1つと捉えられますが、実は「距離が距離たりうるもの」つまり距離の定義(*0)として必須の不等式で，これを三角不等式(*1)と呼びます。
 
・ベクトルにおける三角不等式
平面における2つのベクトル \(\vec{a} ,\vec{b} \) とそれらの大きさについて以下の不等式が成り立ちます。(*2)

\(\left| \vec{a} + \vec{b} \right|≦\left| \vec{a} \right| +\left| \vec{b} \right|\)

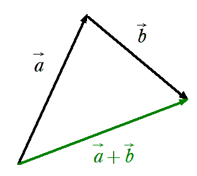
厳密な証明は割愛しますが，以下の図を見ていただくと上記の不等式は「三角形の辺の長さの大小関係」を言い表しているだけということが分かります。
(等号は下の図のような三角形を作ることができないときに成立します。)

複素数平面における三角不等式

2つの複素数 \(z\) ，\(w\) とそれらの絶対値について以下の不等式が成り立ちます。

\(|z+w|≦|z| +|w|\)

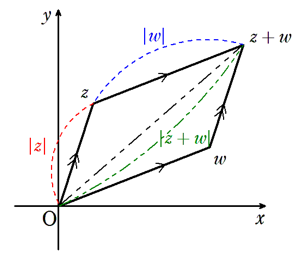
厳密な証明は割愛しますが，以下の図を見ていただくと上記の不等式はベクトルのときと同様に「三角形の辺の長さの大小関係」を言い表しているだけということが分かります。
(等号は下の図のような平行四辺形、三角形を作ることができないときに成立します。)

データの分析における三角不等式

ここまではいかにも「距離」を表すものを扱ってきましたが，変わり種としてデータの標準偏差に関する不等式を見てみましょう。
\(n\) を自然数とします。変量 \(x\) のデータの値が \(x_{1} , x_{2} , … , x_{n}\) ，変量 \(y\) のデータの値が \( y_{1} , y_{2} , … , y_{n}\) により与えられるとき，データの値が \( x_{1} + y_{1} , x_{2} + y_{2} , … , x_{n} + y_{n}\) で与えられる変量を \(x+y\) とします。
変量 \(x\) ，変量 \(y\) ，変量 \(x+y\) の標準偏差をそれぞれ \( s_{x} ,s_{y} , s_{x+y}\) としたとき，以下の不等式が成り立ちます。
(証明は難解ですが，国公立大学の2次試験の対策になるので練習問題としておきます。)

\(s_{x+y} ≦ s_{x} + s_{y}\)

ベクトルにおける三角不等式は「和の大きさは大きさの和以下である」という不等式であり，
複素数平面における三角不等式は「和の絶対値は絶対値の和以下である」という不等式でしたが，
上記の式は「和の標準偏差は標準偏差の和以下である」という不等式と言い表すことができます。

「\(p\) 進距離」と三角不等式

\(d_{p} (x,z) ≦ d_{p} (x,y) + d_{p} (y,z)\)

最後に，この不等式を以下のイメージ図でとらえてみましょう。
( \(x,y,z\) は整数なので，あくまでもイメージ図になります。)

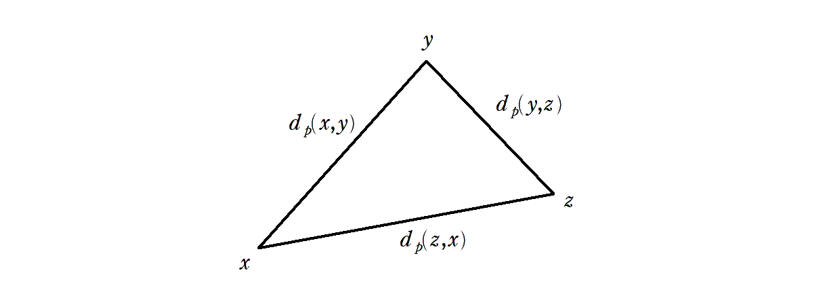
\(d_{p} (a,b)\) を「 \(a,b\) 間の距離」と思うと，これまでの三角不等式と同様に三角形の辺の長さの大小に関する不等式だというように思えます。

最後に

このように不等式1つを取り上げただけでも様々な単元のつながりを観察できます。もちろん，高校生や受験生の皆さんがここまで考えることは難しいですし，入試に合格するために必須の知識ではありません。

しかし，我々京都医塾の講師は今回のように様々な単元を俯瞰して理解しています。

・医学部入試の傾向を常日頃から分析
・受講生のミスを少なくする方法を毎日のように議論
・受講生が気にしないところまで緻密な科目研究

をおこなったうえで教壇に立っています。

他の塾や予備校とは一味違う「京都医塾講師」を体験してみませんか？

京都医塾ではご相談・体験授業を随時募集しています。下記リンクからお気軽にお問い合わせください。

脚注

(*0) 正確には距離空間の定義ですが，他にも満たさなければならない性質があります。\(d_{p} (x,x)=0\) もその1つです。
(*1) 名前は似ていますが三角関数の不等式とは全くの別物です。
(*2)空間におけるベクトルでも同様の不等式が成立します。